Now let’s write down what we have, and what we need, so that we can figure out where to go from here.
So we know: that Kenshin’s mass is 50 kg, the distance he wishes to jump is 3.2 m, the time it will take him to make the jump is unknown (and not needed), his initial velocity (Vi) is unknown (this is what we want), his final velocity (Vf) is 0 m/s (as we are saying that his final velocity is the velocity when he reaches the top of his jump:
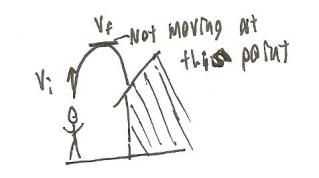
We are specifying that Kenshin’s final velocity (for now) is his movement at the point where he has stopped moving up, and is just about to come back down (If you do not understand this, don’t worry about it too much; it can be rather confusing at first). After that, Kenshin’s acceleration is –9.8 m/s^2 (gravity is negative as we have specified that “up” is the positive direction, so gravity is negative as it is pulling Kenshin “down”).
Phew!
We have the problem setup now! That is quite often the hardest part of a Physics problem. Once you have the problem setup, you can generally see what needs to be done, and simply plug things into equations.
Which is what we shall now do!
The first kinematics equation we shall use is this. Remember that Vf is final velocity, Vi is initial velocity, and that a is acceleration. “d”, is distance (sometimes “u” is also used), and the triangle thingy before it is “delta”, meaning the difference. Therefore “delta d” means the difference, or change in distance.
OK, so now let’s solve this. First let’s rearrange the equation, as we want to solve for Vi. And then we’ll plug in our numbers, and we get our answer! By our situation, Kenshin must be moving at approximately (that is what the = sign with a dot on top means, “approximately equal to”) 7.92 m/s the moment he leaves the ground if he wants to reach 3.2 m in height from his jump.
Another note: we are ignoring air resistance.
Wow! So 7.92 m/s! That is actually VERY fast. If you were running that fast, you’d finish a 100 meter sprint in just over 12 seconds!
But that is just the speed, what we REALLY want is the acceleration that Kenshin must go through to reach this speed. To REALLY understand what Kenshin must have done to move that fast, we need to find the force he must have used to jump. And we already know how to find that! That’s right, Fullmetal Alchemist to the rescue, F=ma!
So how do we find Kenshin’s acceleration? Well acceleration is the change in speed over an amount of time, hence the m/s^2 units: m/s is speed, so your change in speed over an amount of time would be velocity divided by the number of seconds that change took, therefore (m/s)/s = m/(s*s) = m/s^2.
So how do we find this? Well, we have to do a bit of assuming. We know that JUST before Kenshin left the ground, his vertical speed was 0 m/s, but JUST as he leaves the ground, his speed is 7.92 m/s. So when did his acceleration occur? Well, just as he began to push away from the ground. Which is a VERY small amount of time:
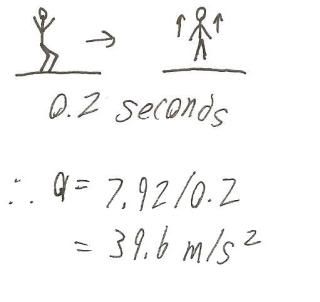
We are looking at the time of his legs extended from his crouching-ready-to-jump position to the moment his feet left the ground. So I’ll be generous here (over-estimate), and say that it took about 0.2 seconds. It probably took much less time, even though that is already a relatively small increment of time.
OK so, Kenshin accelerated 7.92 m/s in 0.2 seconds, therefore his acceleration is: 39.6 m/s^2.
Now THAT is VERY fast. If you accelerated at that speed, it would take you just over two seconds to do the 100 meter sprint! After 10 seconds of accelerating at this rate, you would be moving at a speed of 396 m/s! That’s 1425.6 km/h (or for those of you that use miles, 885.83 miles per hour)! This means that in ten seconds, you would go from not moving at all, to moving at a speed that would allow you to run across Canada in less than 4 hours!
I’m sure all of you can now appreciate the impossibilities that Kenshin must now be doing.
But let’s do one final calculation, this time using F=ma. By plugging in Kenshin’s mass (50 kg) and his acceleration (39.6 m/s^2), we find that the force he must have pushed off the ground with was 1980 N (Newtons).
Now this is harder to appreciate at face value, so let’s do a little calculation. Let’s say that you wanted to move the Kleenex box on your desk 10 centimeters in one second. That would mean that the acceleration would be 0.1 m/s^2. And let’s also say that you wanted to use the force that Kenshin used.
Therefore, we rearrange F=ma to m=F/a, and solve for the mass that the Kleenex box must be if you are going to move it with the same force, but at 0.1 m/s^2. This means that the box must weight a whopping 19 800 kg! That’s around the weight of four elephants (with an average elephant weighing at 5000 kg)!
Now this is harder to understand, but just think of it this way: the force at which Kenshin pushed off of the ground was also enough to move four elephants 10 centimeters in one second!
If it still isn’t getting through, don’t worry. Our other calculation is also just as valid, and unreal (doing the 100 meter sprint in just over two seconds).
Now I’m no biologist, but I’m PRETTY sure that these feats are impossible for humans. So therefore, BY SCIENCE (specifically Physics), we have PROVEN that some things that Anime does is impossible for a human on Earth. No “just saying”, no “it’s obvious”, we have the PROOF that it is.
So unless someone moves four elephants and gets it on video, I conclude that the jumping abilities of many anime characters are, by our current situation and standards on Earth, IMPOSSIBLE.
This has been Kastom for Anime Mythbuster.